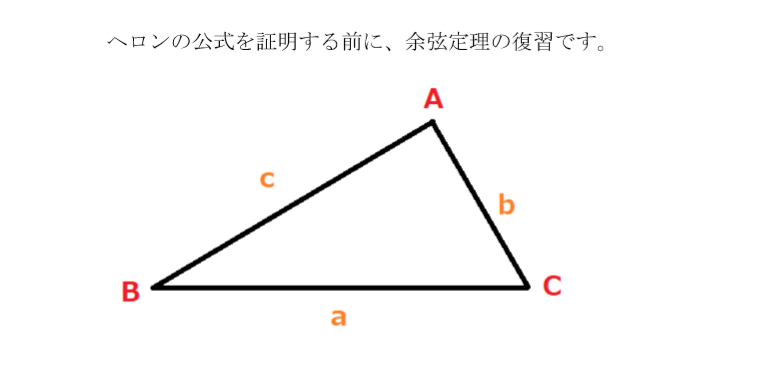
四角形の面積(「ヘロンの公式」応用) 作者 darkn さん 実行数 4940 四角形の面積(「ヘロンの公式」応用) 作者 darkn さん 実行数 4940 が使えますが,ここでは「長さ情報」のみを使用しています. 三角形に分割して「ヘロンの公式」を使っていますので,多角形にも応用できます. 本ライブラリは会員の方が作成した作品です。ヘロンの公式(ヘロンのこうしき)は任意の三角形の3辺a, b, c の長さから面積 T を求める公式。アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる。 16 関係。ヘロンの公式を使わない場合は、 1 余弦定理でひとつの角の$\cos$を得る 2 $\sin^{2}\theta\cos^{2}\theta=1$を用いて、その角の$\sin$を得る 3 復習の2番目の公式を使って面積を求める という手順になる。 余弦定理より、

ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ
ヘロンの公式 四角形
ヘロンの公式 四角形-ヘロンの公式 計算機が見つからず、手計算でやるかと思いましたが、検索してありました。 助かりました。 単一三角では便利ではありますが、通常舗装面積等は多くの三角形に集合体になります。 入力欄を増やす事は出来ませんでしょうか。 尚且つ集計も同時に出来れば大変便利なものになると思います。 非常に助かりましたありがとうございました。 多角ヘロンの公式(ヘロンのこうしき)は任意の三角形の3辺a, b, c の長さから面積 T を求める公式。アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる。 16 関係。


日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式
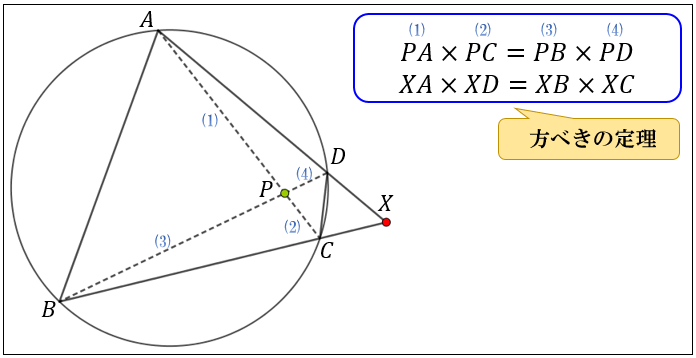
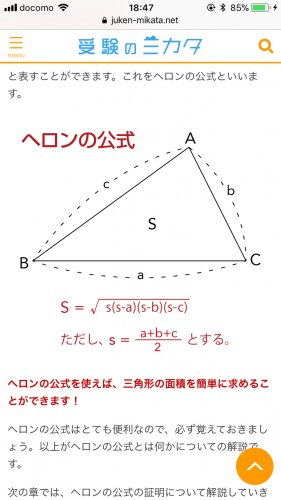
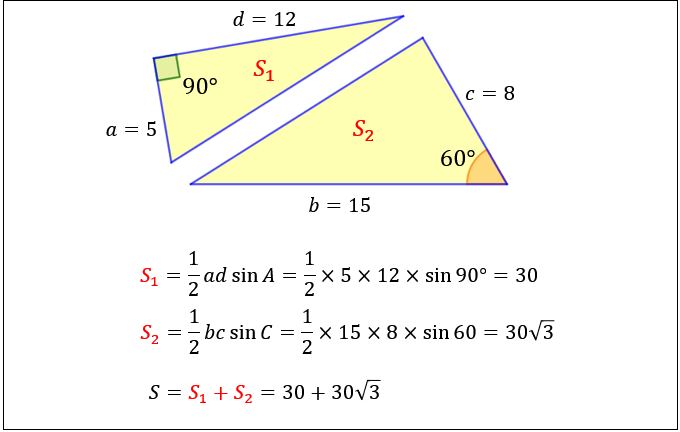
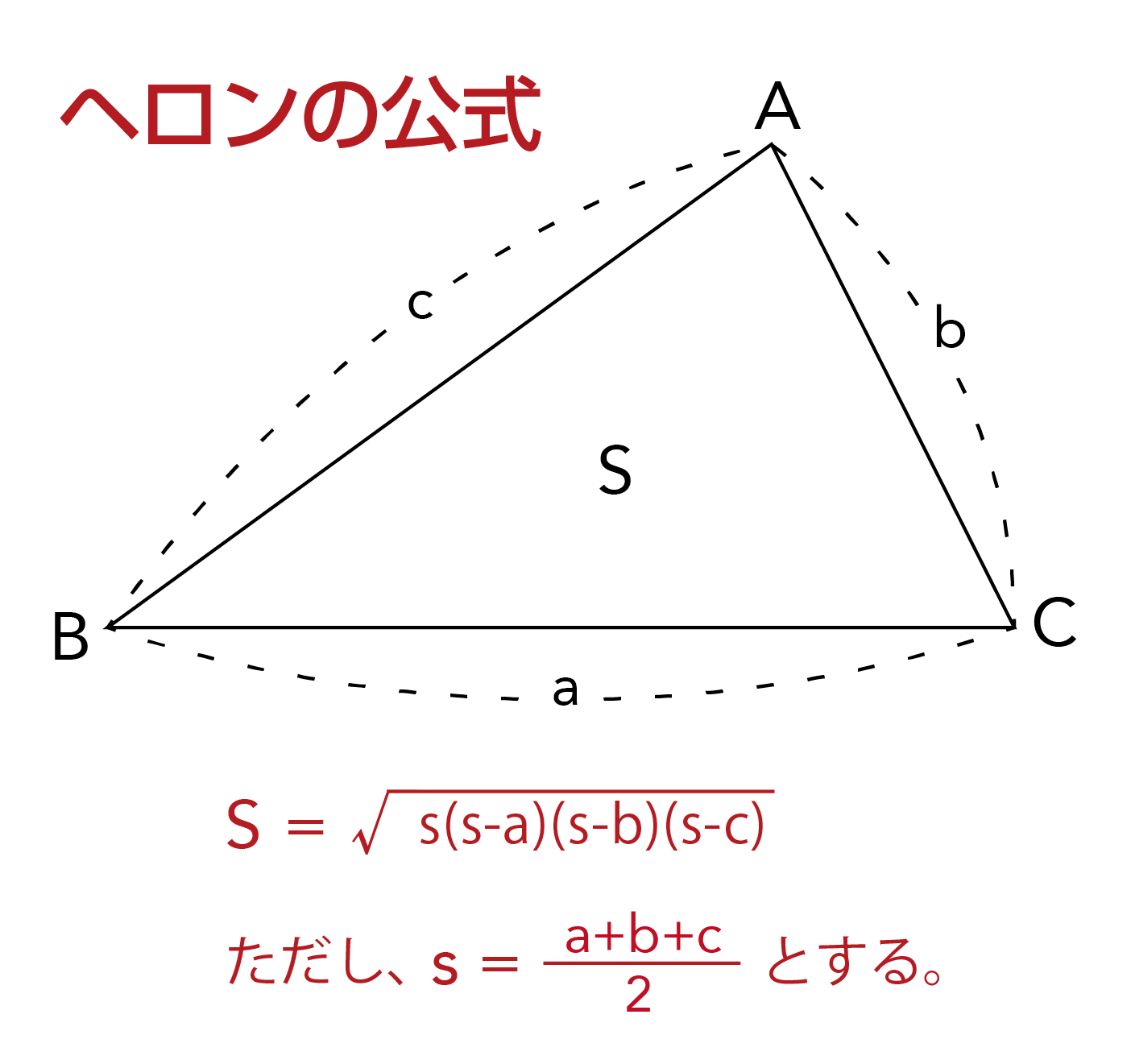
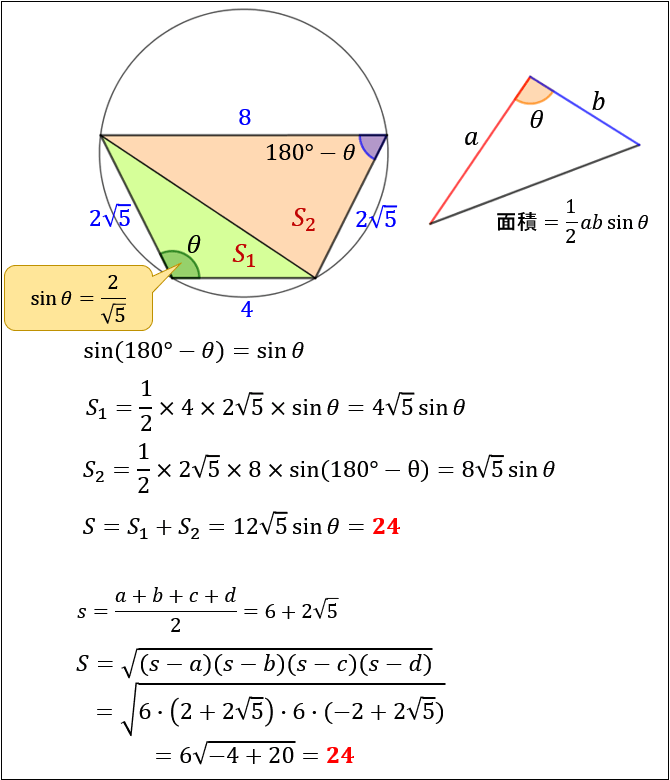
円に内接する四角形の面積を瞬時に求める公式です。 ヘロンの公式と同様,まず $s$ を求めてから面積 $S$ を計算します。 ちなみに,$d\rightarrow0$ の極限を取ればブラーマグプタの公式はヘロンの公式と一致するので,ブラーマグプタの公式はヘロンの公式を含んでいます。四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。ヘロンの公式とは、三角形の3辺の長さ a, b, c を使って素早く三角形の面積を求める公式です。 3辺の長さが a, b, c の三角形の面積 S は S = s (s − a) (s − b) (s − c) ただし、 (た だ し 、 s = a b c 2)
ヘロンの公式 の用例・例文集 円の内接四角形の面積を求めるその式は、ヘロンの公式を内包している。ヘロンの公式はこれらの公式の特別な場合となっている。これは三角形におけるヘロンの公式を一般化したものである。これは三角形の面積を辺の長さで表すヘロンの公式と面積公式をヘロンの公式とは ヘロンの公式とは、三角形の三辺の長さのみの情報からその面積を計算できる式のことを指します。 具体的には、 s=1/2(abc)とした場合に、面積S=(s(sa)(sb)(sc))^05 で表すことができる計算式がヘロンの公式です。3ブラーマグプタの公式 四角形は4辺の長さを与えてもその形は決まらないので,そのような公式は期待できませんが,四角形が円に内接するとき,面積は最大値をとり,ブラーマグプタの公式 この定理でd→0とすると,三角形のヘロンの公式
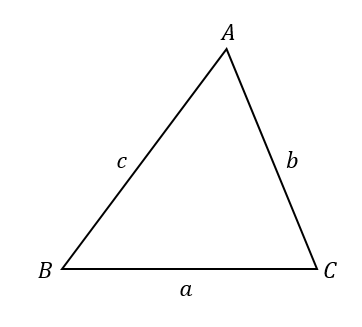
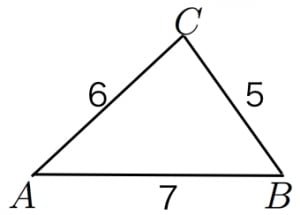
ヘロンの公式・三角関数 三角形の面積の求め方には、他にヘロンの公式と三角関数の利用もあります。 ヘロンの公式 ヘロンの公式 は、三角形の3辺の長さから面積を求める公式です。 3辺の長さが a・b・cの三角形の面積Sは、次の式で表されます。 s=(abc(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。ヘロンの公式で求めた面積は、他の方法で求めた面積と等しいはずだということを使います。 例 三角形の3辺の長さが,それぞれ13,14,15のとき,内接円の半径を求めなさい (答案) s=()/2=21 ヘロンの公式により、S= 他方,S=21r



円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する


ヘロンの公式なんですが Sって面積のことですよね なのにs 2分のa B 高校受験 教えて Goo
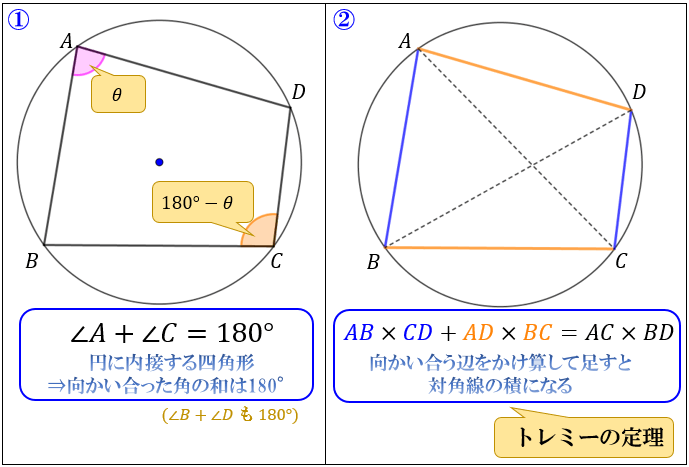
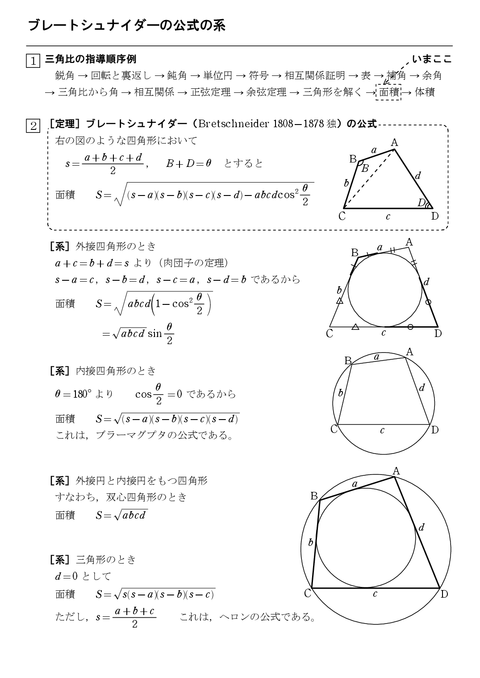
概要 ブラーマグプタの公式は、7世紀にインドの数学者 ブラーマグプタがヘロンの公式の一般化として得た定理である。 ヘロンの公式は三角形の3辺の長さから三角形の面積を求める公式であるが、ブラーマグプタの公式は四角形の 4辺の長さから四角形の面積を求める公式である。実は、ヘロンの公式には四角形バージョンがあり、「ブラーマグプタの公式」といいます。 ヘロンの公式はどんな三角形にも当てはまりますが、ブラーマグプタの公式は 円に内接する四角形限定 です。この等式をブラーマグプタの公式という。 三角形を四角形の特別な場合と見て a = 0 とし、この定理の条件の円を三角形の外接円と考えればヘロンの公式が得られる。 さらにこの四角形 ABCD が円に外接するとき、いわゆる双心四角形の面積 S は S = √ abcd と表せる。


数学 図が高い 二人羽織で はかる線 道路にのびるはヘロンヘロンな図形 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ


ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ
ヘロンの公式とは,三角形の3辺の長さから面積を求めるための公式です。 3辺の長さが a, b, c の三角形の面積 S は, s = a b c 2ヘロンの公式の n 次元版はCayleyMenger Determinantとして知られている 。 n次元版ヘロンの公式(CayleyMenger Determinant) ― n 次元 単体 の体積 V {\displaystyle V} は、 n ( n 1 ) 2 {\displaystyle {\frac {n(n1)}{2}}} 辺の長さによって次のように書かれる。三角形の面積を辺のみの数値から求める方法 ヘロンの公式とは、三角形において角度がわからず辺のみの数値がわかっている場合の面積を求めるための公式といえます。 三角形の辺の長さをx,y,zとしましょう。 さらに面積S(ラージS)を計算する前に、s



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ


コラム ヘロンの公式 江戸の数学
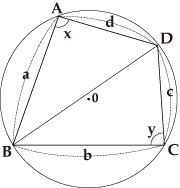
四角形の4辺の長さをa,b,c,d,内角をα,β,γ,δとする.ここで,2s=a+b+cとおくと,四角形の面積は S^2=(s-a)(s-b)(s-c)(s-d)-abcd(1+cos(β+δ))/2 となる. この定理でd→0とすると,三角形のヘロンの公式S = √s(s− a)(s−b)(s−c) ただし s = a b c 2 S = s (s − a) (s − b) (s − c) ただし s = a b c 2 それでは、この 公式の導出方法 と、 ヘロンの公式を使った計算例 について、見ていきましょう。(ヘロンの公式の証明の途中式(※)のルートの中身を整理することで得られます。 例題3 三辺の長さが 5 , 7 , 3 \sqrt{5},\sqrt{7},3 5 , 7 , 3 であるような三角形の面積を求めよ。
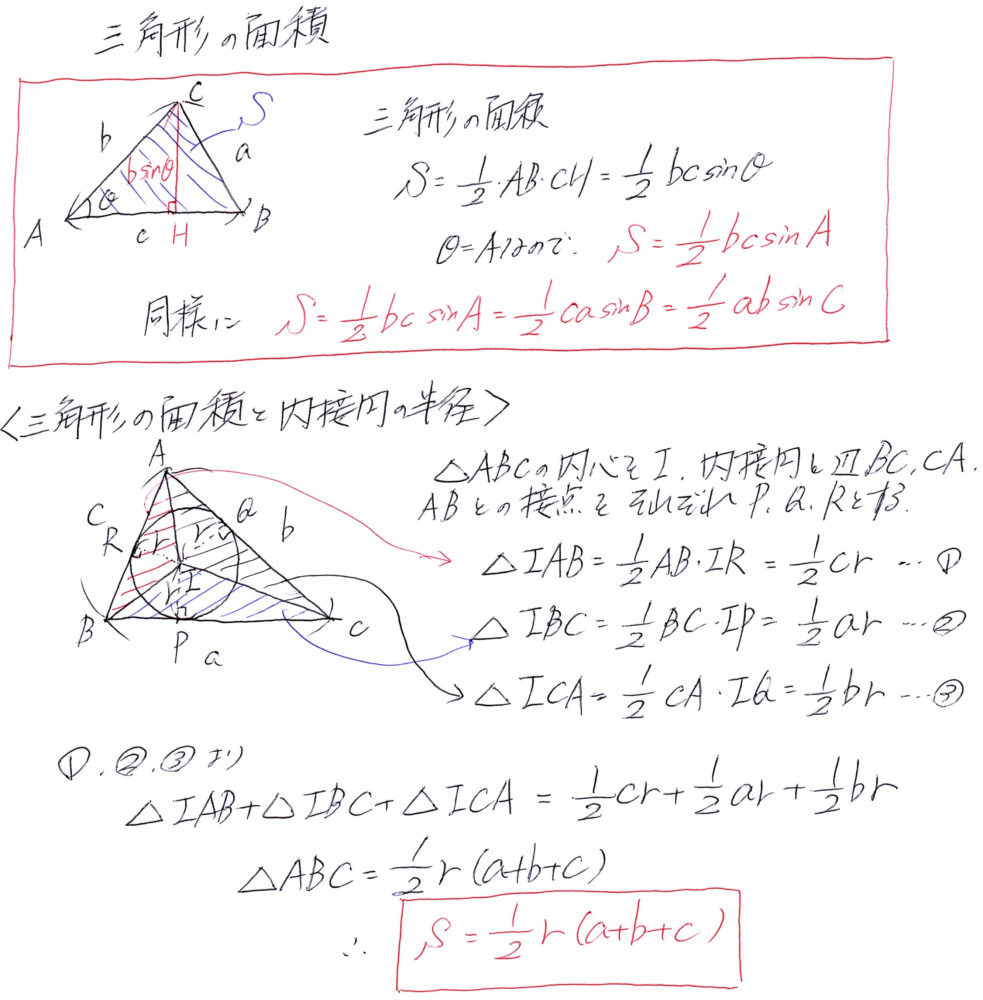


三角形の面積と形状 富岡市の総合学習塾 トータルアカデミー


ヘロンの公式の証明と使用例 高校数学の美しい物語
三角形の3辺の長さを入力 辺 a = 3 辺 b = 4 辺 c = 5 面積 S = 6000 このように直角三角形の面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。ヘロンの公式 の用例・例文集 円の内接四角形の面積を求めるその式は、ヘロンの公式を内包している。ヘロンの公式はこれらの公式の特別な場合となっている。これは三角形におけるヘロンの公式を一般化したものである。これは三角形の面積を辺の長さで表すヘロンの公式と面積公式を


三角形の面積 3辺からヘロンの公式 高精度計算サイト
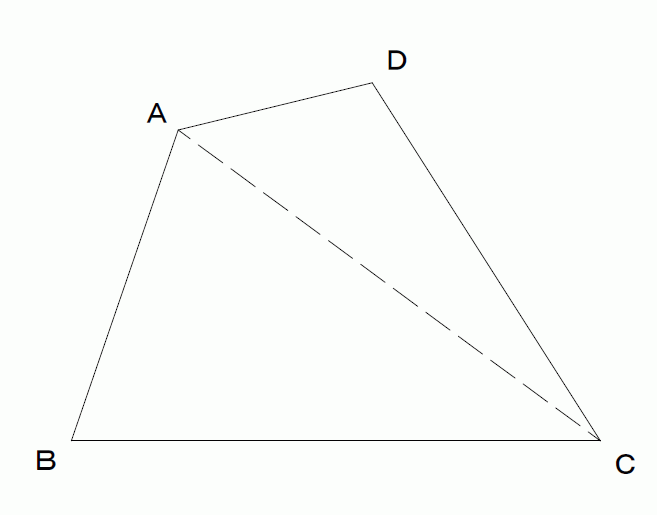


四角形の面積 ヘロンの公式 応用 高精度計算サイト
さらに外接円と内接円を持つ四角形、つまり双心四角形については、 S = √ pqrs となる。また、上記の証明は p = 0 として三角形の面積を考えているとしても通用し、ヘロンの公式 S = √ T(T − q)(T − r)(T − s) を得る。 関連項目 四角形;



ブラーマグプタの公式 17年 大阪教育大 数学日和



三角比 怜悧玲瓏 高校数学を天空から俯瞰する



内接四角形の面積とヘロンの公式 小ネタ集 テストにでるすぐに使える数学のウラ技 Youtube
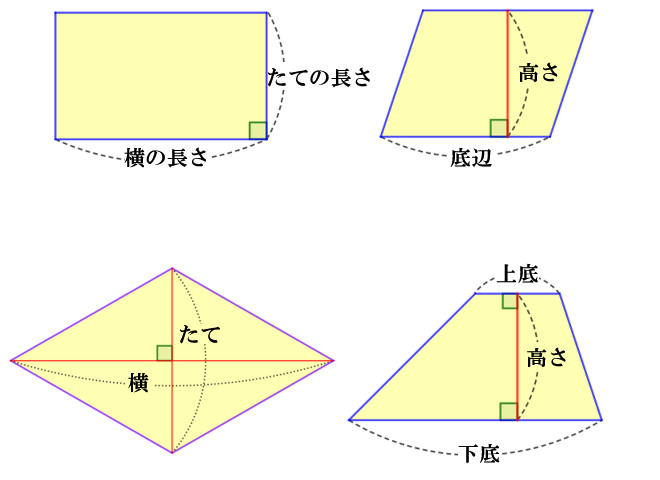


四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
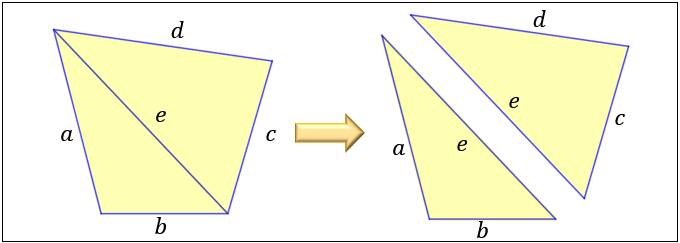


四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



面積の求め方 計算公式一覧
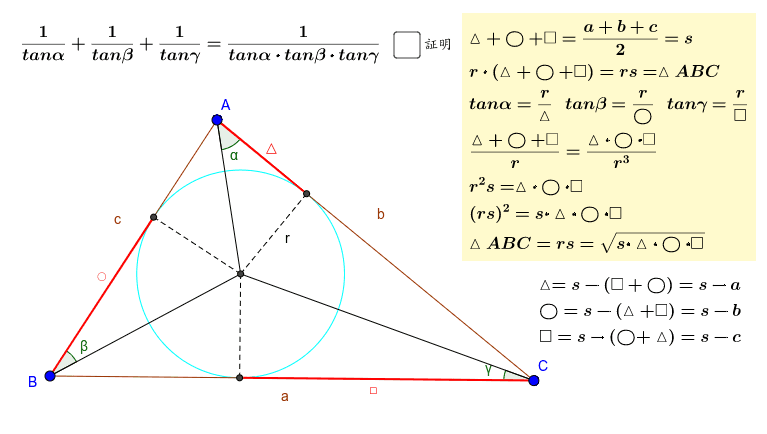


ヘロンの公式 Geogebra



これの 2 はどのように考えればいいですか 答えは ひし形です Clear
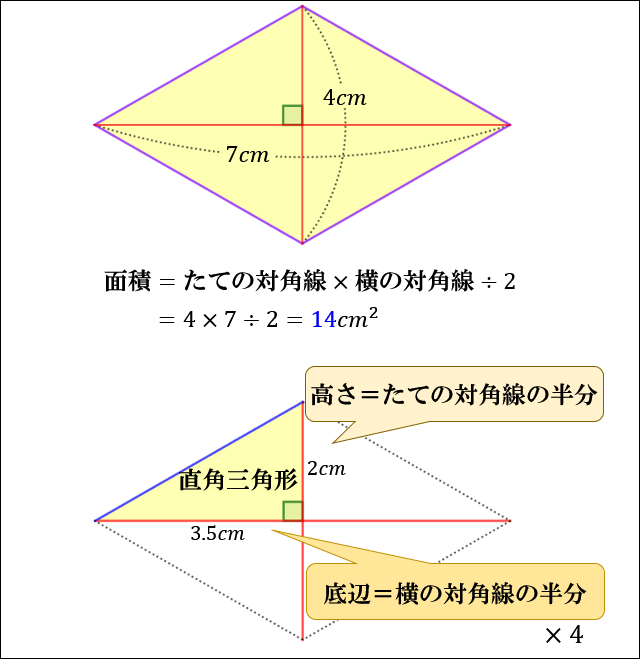


四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
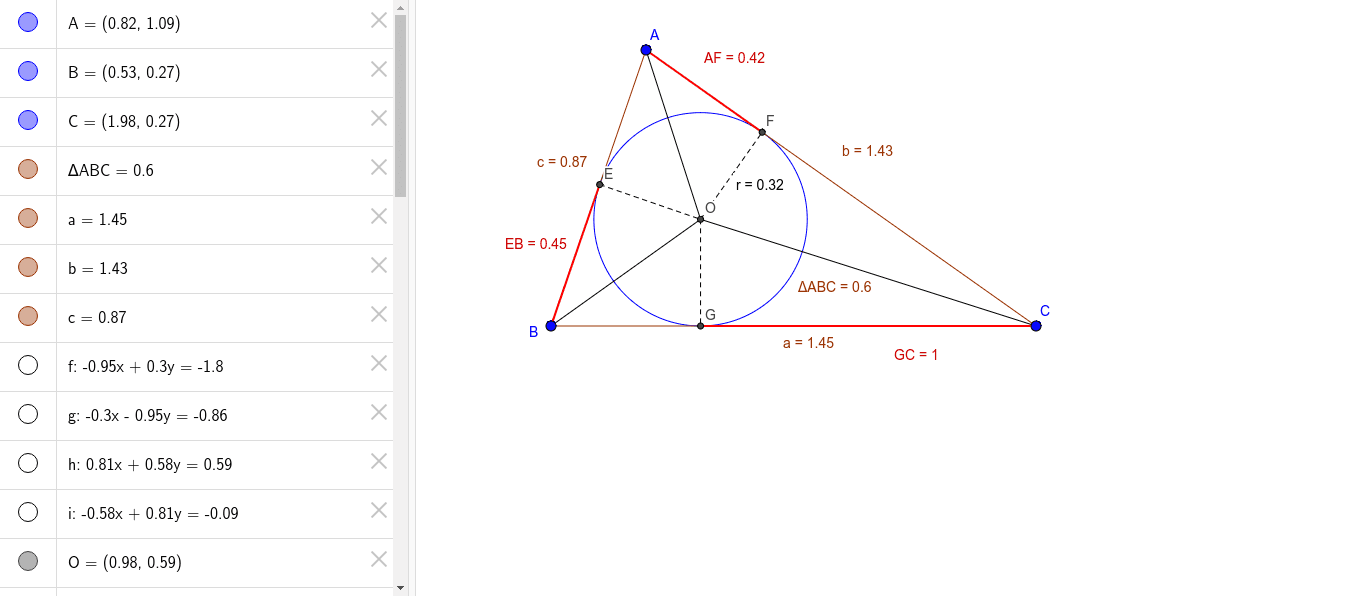


ヘロンの公式 Geogebra



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート


日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式


N Y Cityのまちかど Heron S Formula



標準 三角比と円に内接する四角形 なかけんの数学ノート



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ


面積分割
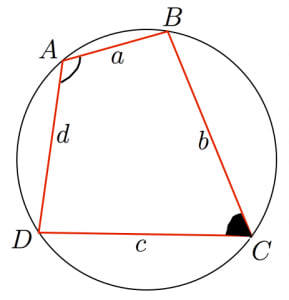


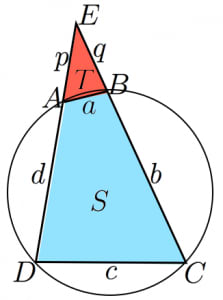
ブラーマグプタの公式とその2通りの証明 高校数学の美しい物語


面積最大の四角形



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ
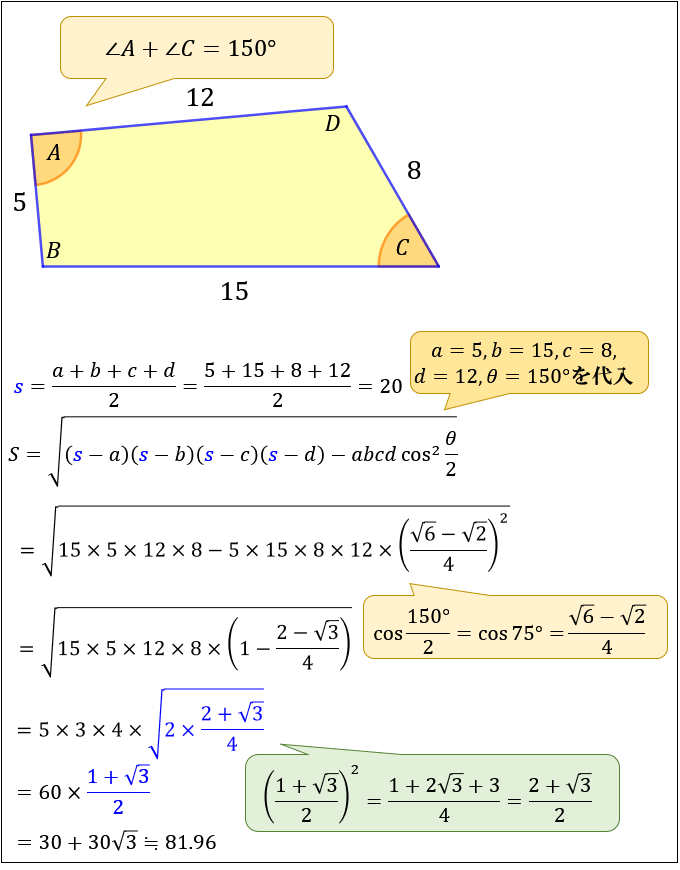


四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート



ヘロンの公式とブラーマグプタの公式をまとめてみました 算数 数学専門塾 算数の極意


N Y Cityのまちかど Heron S Formula



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ



ブレートシュナイダーの公式 Wikipedia
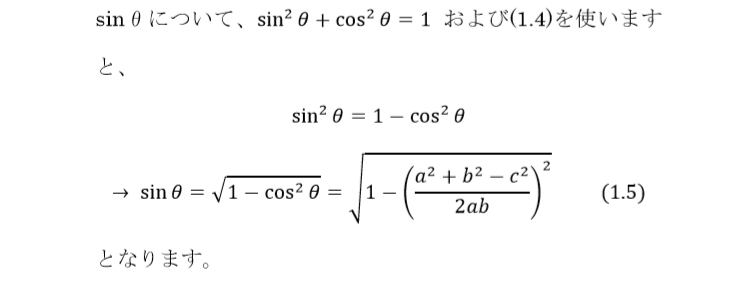


ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ


数学 図が高い 二人羽織で はかる線 道路にのびるはヘロンヘロンな図形 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ



ヘロンの公式 Wikipedia
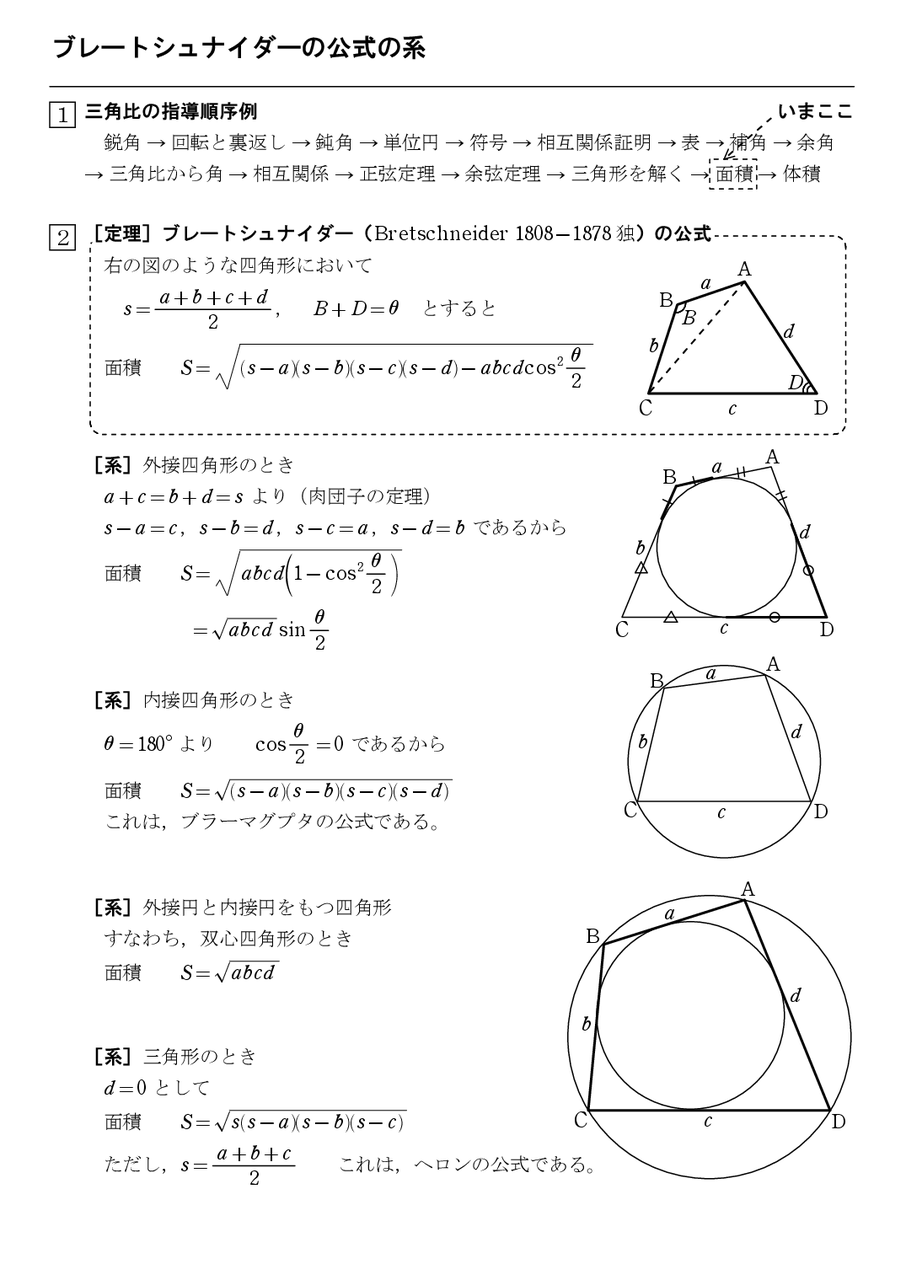


ブレートシュナイダーの公式の系と双心四角形のかき方 怜悧玲瓏 高校数学を天空から俯瞰する
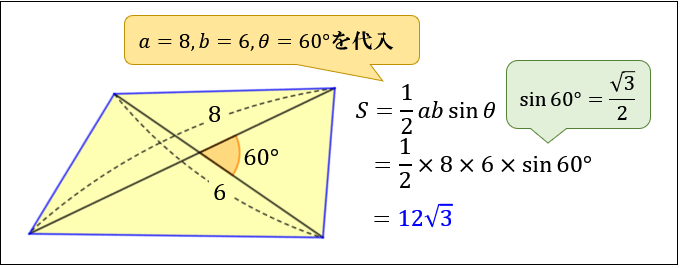


四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
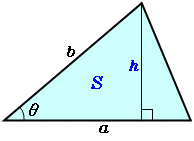


三角形の面積 2辺と夾角から 高精度計算サイト


ブラーマグプタの公式とその2通りの証明 高校数学の美しい物語
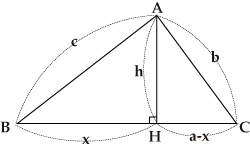


コラム ヘロンの公式 江戸の数学



高1 四角形の面積 ブラーマグプタの公式etc 高校生 数学のノート Clear
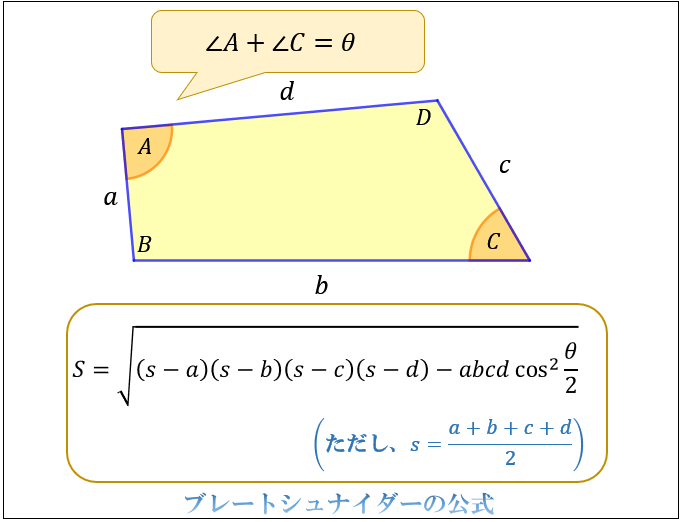


四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式
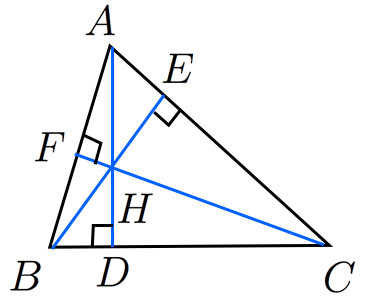


日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式


三角比の面積 公式と計算方法は いろんな場面での使い方を解説 数スタ



高1 四角形の面積 ブラーマグプタの公式etc 高校生 数学のノート Clear


四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



79 ヘロンの公式 三角形と内接四角形 両方解説 ブラーマグプタの公式 Youtube



ブラーマグプタの公式 17年 大阪教育大 数学日和


100 ヘロン の 公式 中学 人気のある画像を投稿する


ヘロンの公式の証明と使用例 高校数学の美しい物語


四角形の面積の求め方について質問です平行四辺形ではないいびつな四角形 Yahoo 知恵袋


四角形の面積を求めたいとき 4辺の長さが分かっているだけでは面積を Yahoo 知恵袋


15年08月 怜悧玲瓏 高校数学を天空から俯瞰する



ブラーマグプタの公式 17年 大阪教育大 数学日和
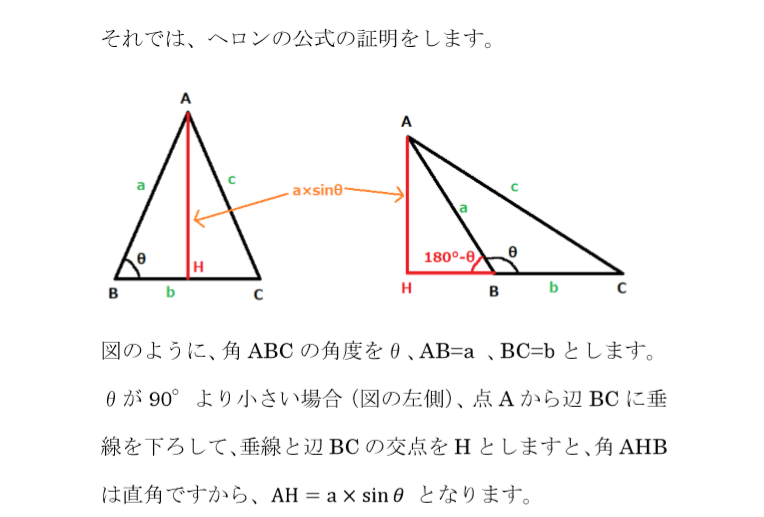


ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ
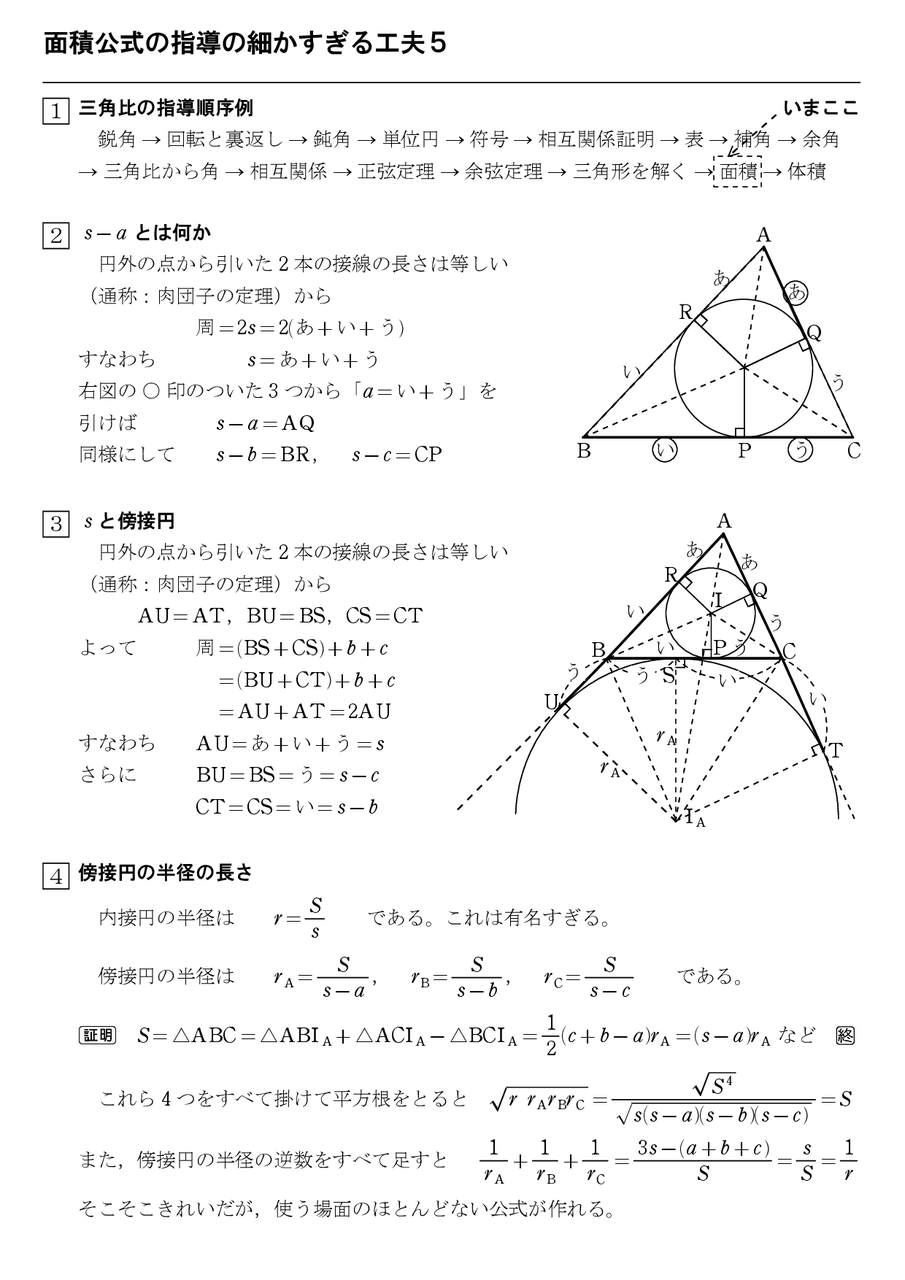


円に内接する四角形の面積 ブラーマグプタの公式 怜悧玲瓏 高校数学を天空から俯瞰する


ヘロンの公式の簡単な証明はありますか Quora



ちょっと中学 高校数学 ヘロンの公式とブラーマグプタの公式 Youtube


数学も英語も強くなる 意外な数学英語 Unexpected Math English December 18



高校数学 円に内接する四角形の面積ブラーマグプタの公式 裏技 の証明と円に内接しない四角形の面積ブレートシュナイダーの公式 裏技 受験の月



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ


日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式



青い下線が引いてある問題の 半径rの求め方が分かりません 高校数学に関する質問 勉強質問サイト
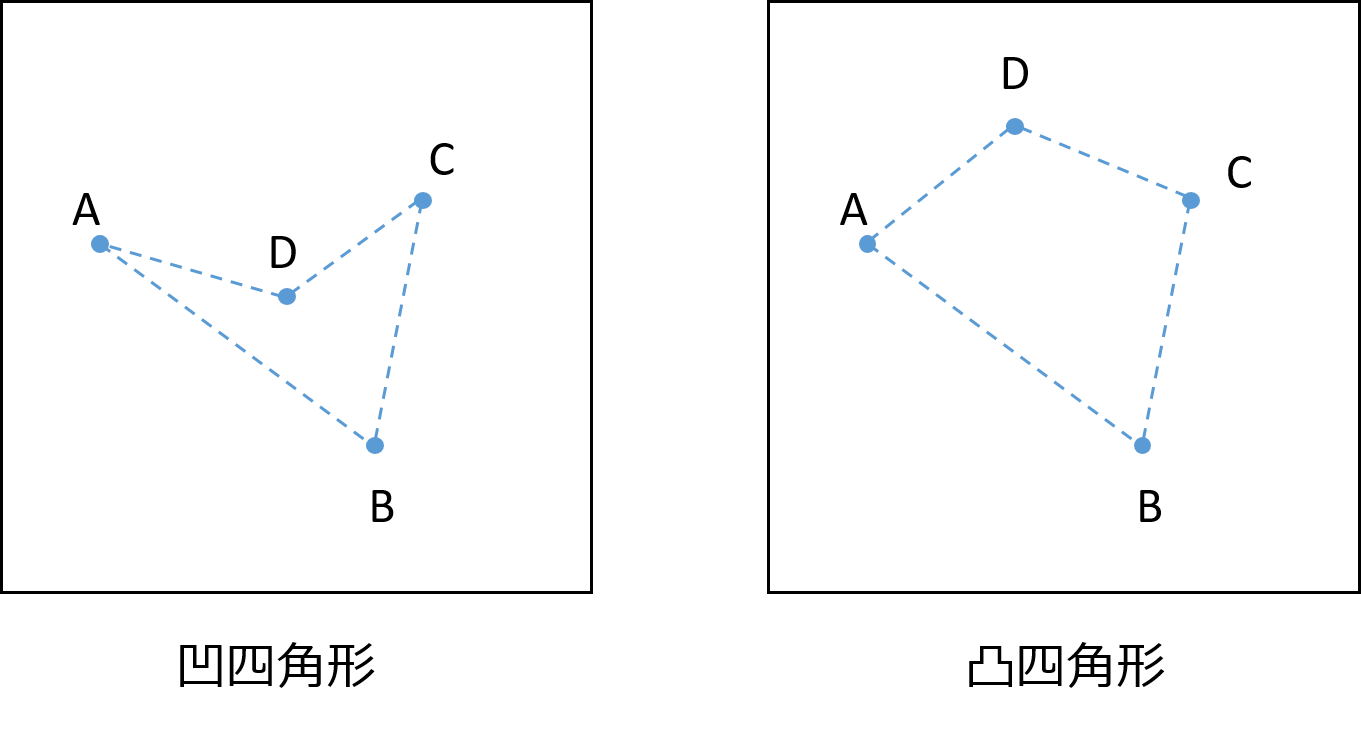


正方形の中にある三角形の面積の平均 Musyokutoumei



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ



L A Twitteren ヘロンの公式とその発展版です 四角形が内接しているというのが条件ですが ヘロンの公式を覚えていると どちらも非常に似てるので 関連付けると覚えやすいです ヽ ー ノ 数学 数検 高校数学



高1 四角形の面積 ブラーマグプタの公式etc 高校生 数学のノート Clear



高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月



ブラーマグプタの公式 円に内接する四角形の面積 大学入試数学の考え方と解法



19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ


15年08月 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式 三角形の面積を求める 数学のカ


4点の座標から面積



図形と計量 の記事一覧 受験辞典


Kadai78



ヘロンの公式 三角形の3辺の長さから面積を求める公式 いまあつ予報士のブログ


数学 図が高い 二人羽織で はかる線 道路にのびるはヘロンヘロンな図形 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ


Grb1f Htm
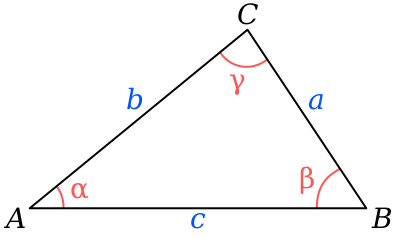


ヘロンの公式 Wikiwand



高校数学 円に内接する四角形の対角線の長さと面積 受験の月
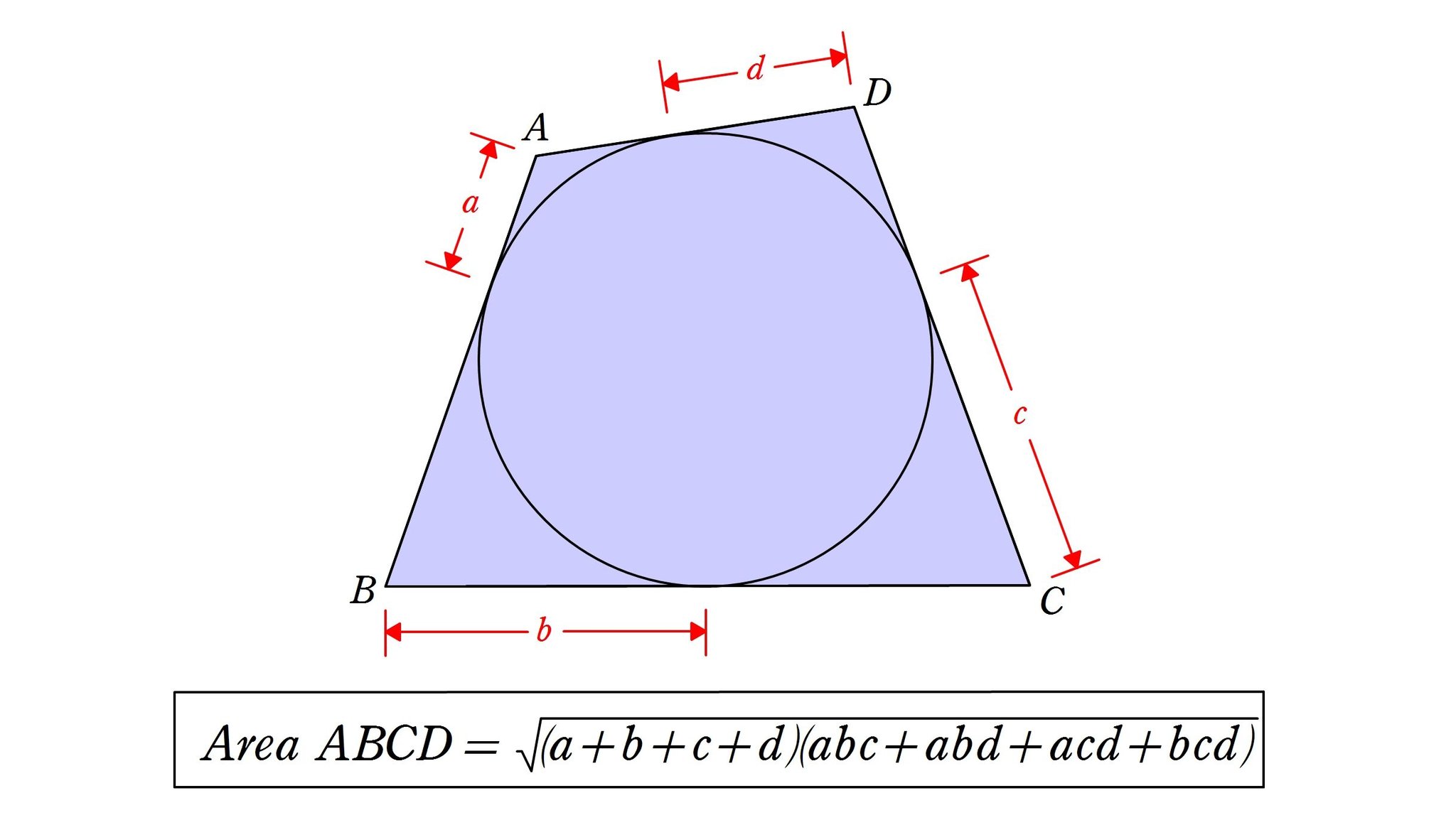


ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
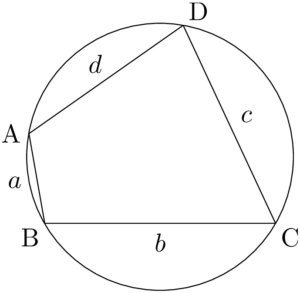


ブラーマグプタの公式 円に内接する四角形の面積 大学入試数学の考え方と解法


三角形の定理 公式の中で 最もマイナーなものは何ですか Quora
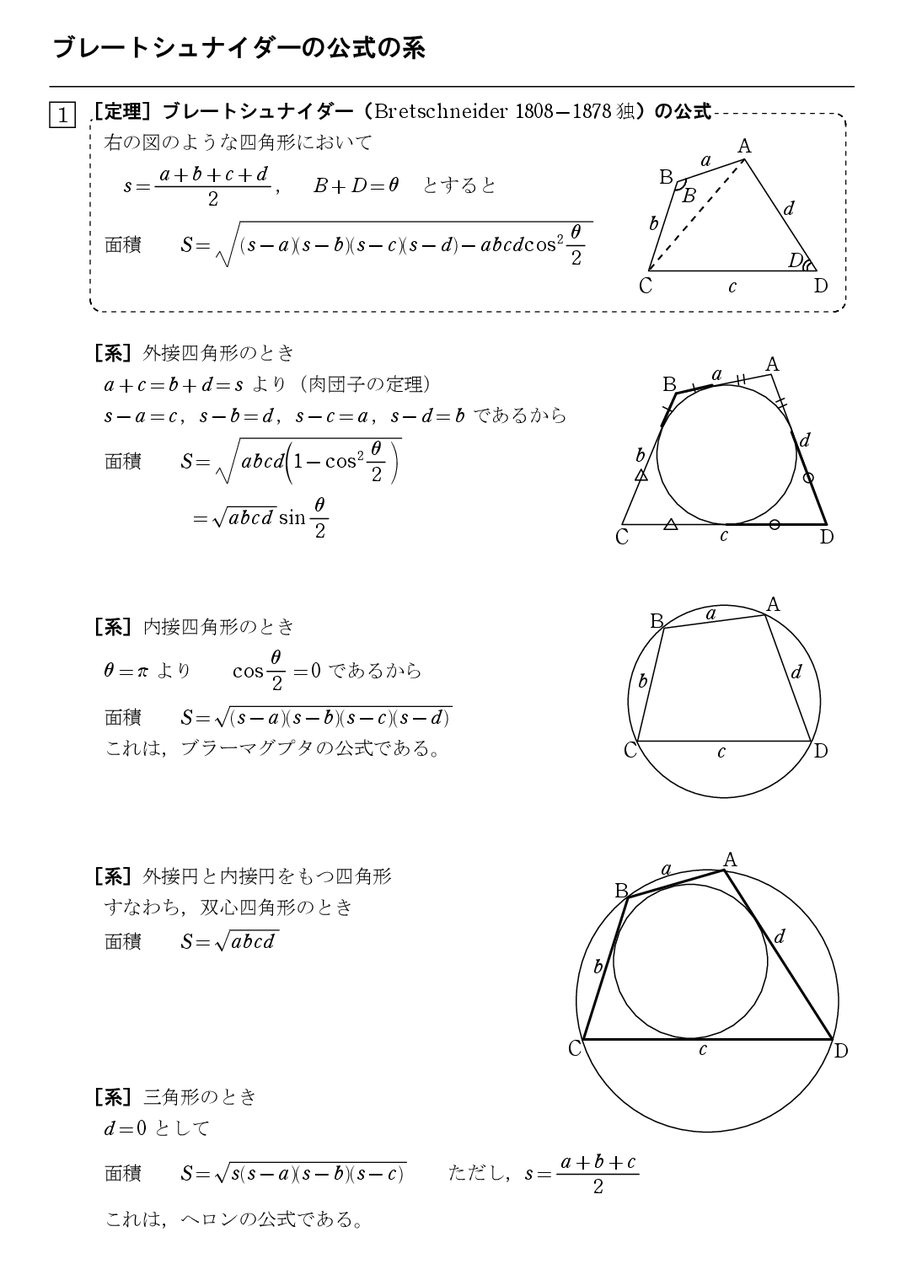


ヘロンの公式の幾何的証明 怜悧玲瓏 高校数学を天空から俯瞰する



ヘロンの公式 オープンデータとgisの匠
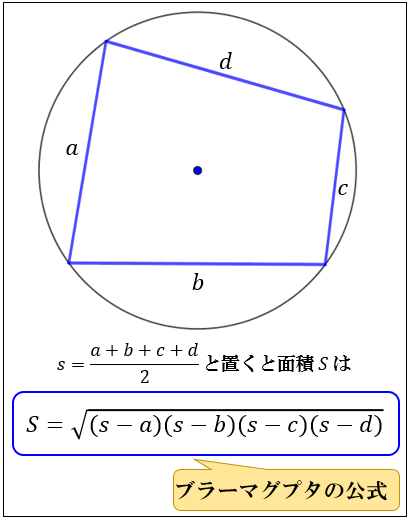


日暮里くん A Twitter ヘロンの公式 三角形の3辺の長さから素早く面積を求める公式 オイラーの定理 内心と外心の距離を求める公式



4点の座標がわかっているときの四角形の面積 平面上の4点の座標がわか 数学 教えて Goo


ヘロンの公式に似ている四角形の方の公式の名前を教えてください Yahoo 知恵袋



四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
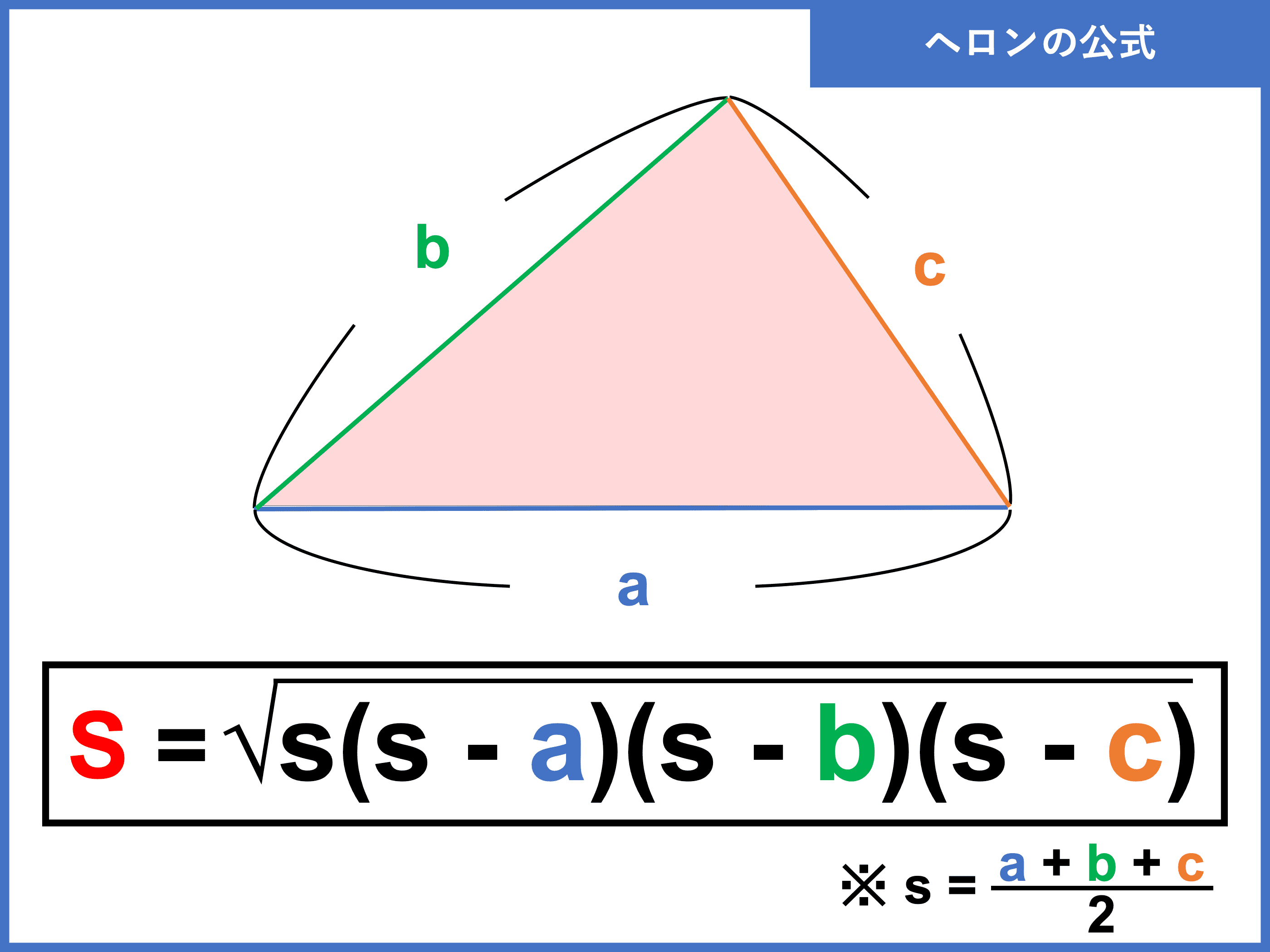


ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典



0 件のコメント:
コメントを投稿